What goes on when a rugby ball is kicked? This is actually a pretty tricky question, and not just because the ball isn’t round! We’ll narrow it down a bit and talk about the spiral and the swerve.

The Spiral

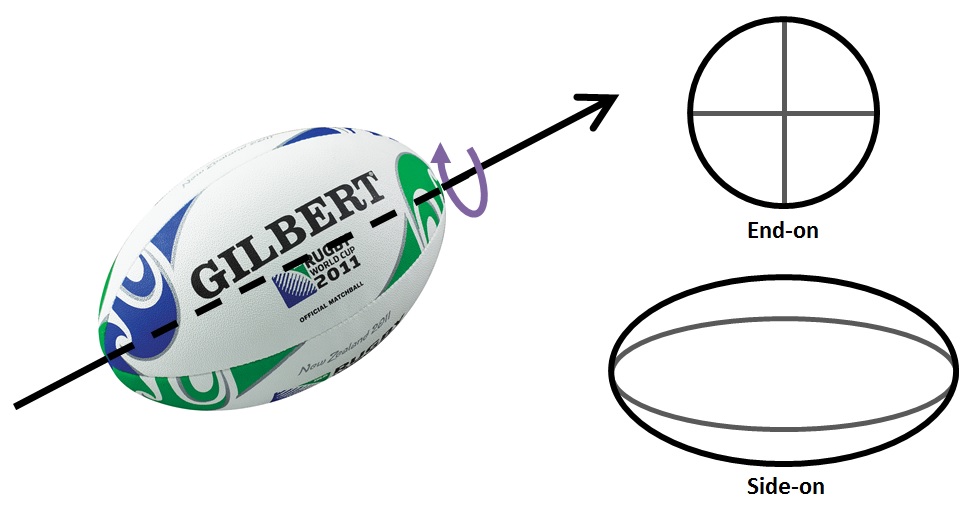
Any budding young first five-eighth learns the spiral punt at an early age. They kick the ball with the outside of their foot so that it spins (purple arrow) around its long axis (black arrow), while travelling in the direction of that axis. Pretty soon these mini-Dan Carters figure out that this style of kick helps them to kick the ball further.*

The ball travels further because the air resistance on the ball is relatively small. Air resistance is like the ‘wind’ you feel when you’re riding a bike. It produces a drag force which slows you down, or makes it harder to maintain a constant speed. The size of the force felt by a particular object depends on its shape – generally, if less surface area is facing the direction of movement, then the force is weaker. This is why you hunch over your handlebars when you want to ride your bike quickly, and why the rugby ball travels further if it stays end-on into the wind, rather than side-on. In the picture above, the area of the ball that you see is much smaller when the ball is end-on to your viewpoint.

If you’ve kicked it right, the punted ball stays with its long axis pointing in the direction of motion as it flies downfield. This position is held stable by gyroscopic forces – the same phenomenon which keeps a spinning top upright. A spinning top looks like it should fall over, but stays upright; in the same way, a spinning rugby ball is prevented from tumbling end-over-end.

The trick to understanding a gyroscope** is angular momentum. Just like any moving object has (normal, or ‘linear’) momentum, any spinning object has angular momentum, and to show it we use a vector pointing in the direction of the spinning axis. In the figure above, the angular momentum vector points along the black axis. To start the ball tumbling end-over-end, angular momentum must be provided in a different direction (in the figure above, the vector might point in or out of the page). The interaction between these two vectors which point in different directions produces a gyroscopic force. This prevents the ball from tumbling, and the spin associated with the spiral punt is preserved.

The Swerve

All kinds of sports fans will be familiar with balls swinging around in flight. Whether it’s Roberto Carlos bending a soccer ball around the wall, a swinging ace at Wimbledon, Shane Warne’s dipping flipper, or a weekend hacker slicing and hooking their golf ball from bunker to rough, the same principle applies. It affects kicks in rugby, and this week it would be wrong to go any further without also mentioning the newly crowned NRL premiership winner Johnathan Thurston and his banana kicks at goal.

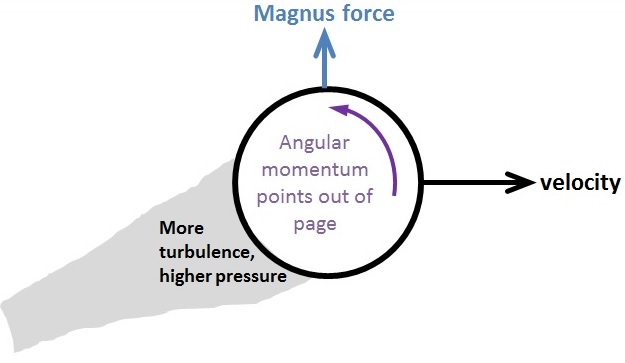
Most of the time, the swerve on a spinning ball is caused by the Magnus effect, which sends the ball sideways because of a difference of pressure on the two sides of the ball. The idea (called Bernoulli’s principle) is that the air pressure is lower where air is moving with higher speed. This applies to aeroplane wings, which are shaped so that the wind speed is greater above the wing, and the pressure difference on either side of the wing forces the plane upwards (phew). The flow of air past a spinning ball is disrupted on the side of the ball which is moving against the oncoming air. There is more turbulence on that side of the ball. There’s a round ball in this picture for simplicity, and the grey area shows where there is slow-moving, high-pressure turbulent air.

The direction of the Magnus force for the spinning ball can be predicted using a right hand rule. For this, we need two vectors. The first is that angular momentum vector caused by the ball spinning, which points out of the page in the figure above. The second vector is the direction of the ball’s motion – here, pointing from left to right. If we take our right hand and curl the fingers so that they turn from the angular momentum vector to the velocity vector, then our thumb will point in the direction of the Magnus force. That means that you’re curling your fingers from a vector pointing out of the page into a vector pointing towards the right, and your thumb points upwards. This is the direction of the Magnus force, and the direction in which the ball will swerve.

* The same is true of the spiral pass, although in that case you also want to consider that your team-mate has to catch the pass … for similar reasons the spiral punt is never really used in Australian rules football.

** Smartphones have very small gyroscopes which act as sensors. These sensors are what tells the phone that it is sitting on its side or being waved around, so that the screen can react accordingly.