Applications are now being accepted for two fully-funded PhD studentships (1 x experimental, and 1 x theory/modelling) to study novel emergent properties of soft matter. Review of applications will begin immediately and continue until the position is filled, with a goal of commencing work in or before February 2017.
Simple soft matter systems can give rise to complex emergent properties such as gelation, and phase transitions, described using elegant theories such as percolation and reptation. With slightly more complex building blocks, we can obtain self-assembled micelles, rods, and bilayers, or produce active matter which is likened to biological swarms. In the era of nanotechnology, micro- and nanoparticles can be designed and engineered to probe further possibilities. This project will use nanotech capabilities, alongside theoretical work, to design, make, and study forms of soft matter with new emergent properties.
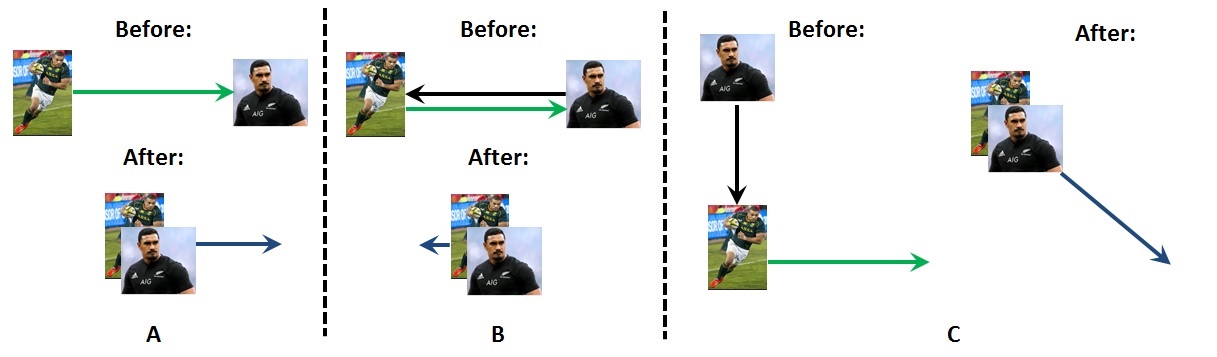
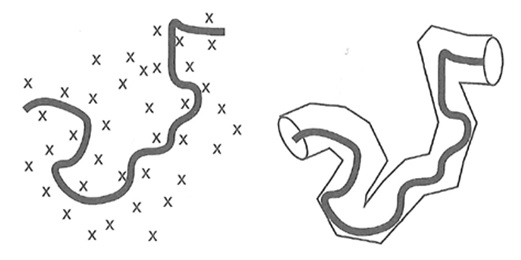
One (experimental) student will use various capabilities (e.g. microfabrication, protein engineering, surface chemistry) to produce particles in solution which assemble and cluster in unconventional ways. Candidate materials could include: (i) Materials with memory, analogous to collections of pedestrians (Figure, left); (ii) Interacting mobile particles, including asymmetric Janus spheres (Figure, right); (iii) Metastable materials which enable switchable transitions. The student will be trained in a wide range of nanotechnology techniques.
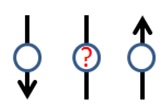
Figure: Left (from [1]), pedestrians travelling up (blue) and down (red) learn to separate over time. Middle and right, TEM images of Janus particles – gold evaporated on to silica – fabricated at UoA (images: Anupama Rao Gulur Srinivas).
Another student will use theoretical and modelling approaches (e.g. molecular dynamics) to understand emergent phenomena observed in the experimental work. This work will also guide the experiments by exploring the possibilities arising from specific particle designs. Universality is a particularly exciting aspect here: analogous systems could be identified within social, ecological, economic, and other complex systems. Computational work will draw upon the University of Auckland’s high performance computing resources.
Projects will be academically challenging, requiring applicants with a strong background in a physical sciences discipline and excellent command of written and spoken English. For the experimental project, laboratory research experience would be an advantage. For the theoretical project, familiarity with collective phenomena and/or high performance computing would be an advantage.
The projects are based in the Departments of Physics and Chemistry at the University of Auckland. Students will benefit from extensive collaborations and thriving postgraduate communities within two of New Zealand’s Centres of Research Excellence: The MacDiarmid Institute for Advanced Materials and Nanotechnology (www.macdiarmid.ac.nz), and Te Punaha Matatini (www.tepunahamatatini.ac.nz). Each student will receive a stipend of $27,000 per annum in addition to course fees.
Applications should include a CV, academic transcripts, and a brief (1 page max) statement of research experience. Applicants must fulfil the University’s English language requirements (www.auckland.ac.nz/en/for/international-students/is-entry-requirements/is-english-language-requirements.html) and should provide the names of at least two people who can provide personal letters of reference.
Contact:
Dr Geoff Willmott
g.willmott@auckland.ac.nz
[1] Morton, N.A. and S.C. Hendy, Symmetry Breaking in Pedestrian Dynamics. 2016: arXiv:1605.05437.