This penultimate (semi-final?) RWC blog takes its name from a regular Friday night feature on The Crowd Goes Wild. Smashed ’em Bro is a countdown of the most spectacular collisions from the week’s sports coverage. In a happy coincidence, Stuff.co.nz got in touch this week to ask about trying to tackle Julian Savea.* You can read about some calculations from last Sunday’s demolition of the French at that link.

When making a tackle, first and foremost let’s make sure that it’s safe. Anyone taking part in a rugby game in New Zealand (playing, coaching, or refereeing) needs to watch Rugby Smart. We have to grasp the player with our arms below the line of their shoulders, and we can’t lift or tip them over so their head or shoulders hit the ground first. The person being tackled must not be jumping in the air, and they must be carrying the ball. If we don’t follow these rules, the next blog will have to be about the optical spectrum of cards in the ref’s pocket.

To get on to the countdown, what we need is drastic change in the speed and/or direction of motion. We can explain most of what goes on in a collision using conservation of momentum: the total momentum after the collision is equal to the total momentum before the collision. From previous blogs, we might remember that p = mv. Momentum is just mass times velocity, and velocity is a vector. So, momentum is also a vector. Here we’re putting vectors in bold type. Momentum points in the same direction as velocity, but its magnitude (arrow length) is multiplied by m.

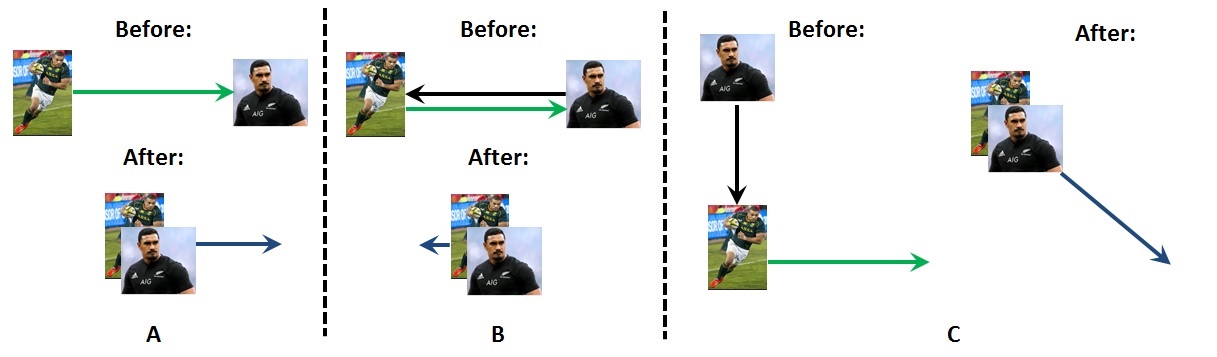
In the Figure (bird’s eye view), we have three cases in which Springbok legend Bryan Habana (H) is running along with a certain velocity (green arrows), and collides with All Black loosie Jerome Kaino (K, black arrows). Initially, we have p = m_H v_H + m_K v_K . This is vector addition, so we have to put the arrows representing m_H v_H and m_K v_K head-to-tail to find the resultant p. After the collision, Kaino and Habana stick together, because Kaino has correctly grasped his opponent. So, the total mass is m_H + m_K, and the final velocity is v = p / (m_H + m_K).

In case A, Jerome is standing still when he makes the tackle (v_K = 0), so p points in the direction that Bryan was running, and afterwards the players move off in that direction. The (blue) velocity arrow is shorter than before the collision, because the mass of both players is greater than the mass of Habana on his own. This is what happens in most tackles, especially in amateur rugby.

In case B, Jerome runs into Bryan at the same velocity, but in the opposite direction. Kaino’s momentum is slightly greater because he’s a forward, so he’s a bit heavier than Habana. When we add the momentum vectors, there is a small resultant from right to left, and the two move in that direction after the collision. This represents a decent change in velocity for Habana, and the collision might make the Friday night countdown.

In case C, Jerome runs towards Bryan at a 90 degree angle. We have to draw a triangle and use some trigonometry to figure out p. The magnitude of p (from Pythagoras) is larger than cases A and B, so the velocity is relatively large following the collision, and at an angle to the original direction of Habana’s motion. This type of collision probably produces the most spectacular changes in direction, and it’s one reason why rugby coaches tell you not to run across-field.

So, collisions will produce large changes in velocity when the two colliding ‘bodies’ are moving fast (running quickly), and have large mass (are big and muscle-y). But the momentum of a collision can be altered by applying forces  – see Newton’s 2nd Law.

This picture shows several players in a scrum, trying to push from right to left. What you might notice is that all the boots are on an angle. To exert a force sideways on the scrum, the players have to sink their boots into the turf so that they can push against the ground sideways.** The same is true at a tackle. A player can change p if they arrange their footwork so that they can push sideways off the ground. Players need to retain their balance: there’s no point pushing strongly while you’re lying flat on your face. Of course, in a tackle everything happens quickly. If players get into a position where they are unable to use their feet to exert a sideways force, they are at the mercy of their opponent.

To make a spectacular hit, you can now start to think about whether the tackler wants to make contact high or low (if you know about torque, you can throw that in the mix), and whether the ball carrier is better off with their feet on or off the ground. Once you’ve got it all sorted, you can analyse this.

You can leave questions / comments / suggestions here or @GeoffWillmott. Source note: some material is based on the book “The Physics of Rugby” by Trevor Davis Lipscombe (Nottingham University Press).

* Although Stuff is motivated by scaremongering, it’s good that Doug King gets a plug in that article for his excellent work on concussion in rugby.

** This is why forwards have longer studs on their boots than backs. It might slow them down a little when they are running, but it is more important that they are able to grip and push in the scrums.