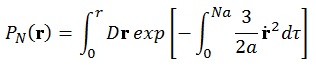Prof Sir Sam Edwards passed away earlier this month. Notable obituaries have been written by Cavendish Laboratory colleagues of Edwards, Prof Athene Donald (here and here), and Prof Malcolm Longair (here).

Reading some of the tributes to Edwards, it occurred to me that his work has had more influence on me more than I had thought. He was a mentor to some of my mentors – in New Zealand we might call this academic whakapapa. His ideas figured heavily in my undergraduate literature review on spin glasses, in an honours course I took on theoretical methods, and most recently in the polymer physics I teach at Auckland. I thought I’d record a couple of reflections on Edwards’ work as I have come across it.

Edwards is most well-known for his work in Soft Matter Physics, an area which superficially appears …. well, tricky. Physics students (broadly) progress from considering single items and phenomena, to well-ordered crystals with many atoms, and to continuous gases and liquids. In Soft Matter Physics we describe milk, snot, rubber, plastics and food: systems with disordered microscopic components (like a fluid) which may interact strongly (like a solid). Our PHYS354 course includes a module on Soft Matter Physics, and this area stands to play a significant role in continuing research here at Auckland and within the MacDiarmid Institute.

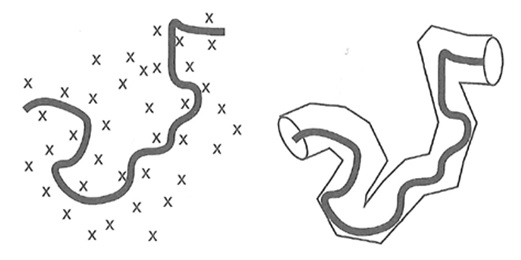
A key example of Edwards’ work is the rheology (or, mechanical properties) of polymers. Unlike elastic solids, polymers do not return to their original positions after being strained. They do not flow freely like a simple liquid (e.g. water). Their mechanical properties depend on how they have been strained previously, and how fast they have been strained; they are viscoelastic and non-Newtonian. The theory of reptation, which can be used to explain how polymers deform, is most easily associated with 1991 Nobel laureate in physics, Pierre Gilles de Gennes – particularly as the theory is so elegant that it appears stereotypically French! However the credit is shared principally with Edwards (who was Welsh) and Masao Doi (who is Japanese).

Polymer molecules are long and thin, so that a mixture can be thought of as a plate of spaghetti (or perhaps a can of worms). In reptation, each polymer strand is confined to a tube formed by the other strands, and theoretical approaches can progress from there.

[Images from R.A.L. Jones, Soft Condensed Matter, Oxford University Press (2002).]*

As an example of one of the ways this is expressed mathematically, consider the following equation, which can be used to calculate the probability P that a polymer strand (a chain with N links of length a) has an end-to-end vector r:

This calculation known as a path integral; the notation “Dr” represents an integral over all the possible ways of obtaining the vector r between the start and end of the chain.

Edwards introduced this path integral approach to polymer physics in a series of papers through the 1960s. The remarkable part is that the theory is borrowed from a field-theory approach to particle physics: the same calculation will find the probability that a quantum mechanical particle goes between particular initial and final states. All you have to do is replace the chain length Na with a length of time T, and change the constants in the exponent to include a particle’s mass and Planck’s constant. Applying this technique to polymer physics is powerful:

• Path integrals can be represented by intuitive diagrams. In particle physics, these are known as Feynman diagrams, and Edwards extended their use to soft matter.
• Further tools from particle physics (especially application of fields to the particle) can be imitated in order to represent the interactions between polymer strands, as in reptation.

The use of an idea developed for one purpose to describe a completely different problem plays an important role in physics, and has been called universality.** There is another nice example of universality from Edwards’ work, this time relating to his development (with Philip Anderson in the 1970s) of theory relating to a class of material called spin glasses.

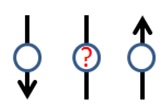
In spin glasses, atoms are spatially arranged in a nice ordered crystal lattice, but the arrangement of their magnetic spins is the tricky part. Each atom has a spin that can be thought of as a little arrow pointing in a particular direction. Interactions between neighbouring atoms give rise to rules, for example, “if the atom next to me has spin pointing up, then I should have spin pointing down, and vice versa.” Spin glasses arise when the atoms are arranged so that the rules can’t be followed – for the example above, if I am an atom placed next to two neighbours with spins pointing up and down, what am I to do?

This phenomenon has a most apt and evocative name – it is said that the spins are frustrated. For large collections of atoms, the problem can be approached by arranging the spins to minimise the energy (the amount of frustration) in the system. This is a difficult problem, because many different arrangements of the spins have low energy, but it is not clear which has the lowest. Physicists often talk of an energy landscape: a rolling plain in which there are many hills and valleys, but the plain is so large that it is difficult to tell where the lowest point is. This problem, and Edwards’ approach to it, also has strong universality, and can be applied to problems as diverse as neural networks and the travelling salesman problem.***

So that’s a couple of examples from the work of Prof Sir Sam Edwards, who is known for application of field theories to soft matter, development of a theory for polymers in particular, and introducing us to spin glasses. For more about Edwards’ scientific contributions, there’s a book called Stealing the Gold. If you are looking for the copy in the University of Auckland General Library, you might have to wait a little while.

* This is our PHYS354 textbook. Jones, who studied with Edwards at Cambridge, is now Professor of Physics and Pro-Vice Chancellor at The University of Sheffield.

** Universality is an important aspect of complex systems, a field being studied by Te Pūnaha Matatini, which is based here in the Department of Physics at Auckland.

*** If a salesman must visit every house in a neighbourhood, which is the shortest route to take? Solving this problem efficiently is an important problem in maths and computer science.